この記事でわかること
・モンテッソーリ教具【三項式の箱】の仕組みとは?
・【三項式の箱】のお仕事の目的とは?
・【三項式の箱】から得る効果とは?
この様な疑問をお持ちの方に、
画像多めで解説してみようと思います。
4年間モンテッソーリ園に通っている中で、
息子が3〜4歳児クラスの時に夢中になっていたお仕事です🌟
文系で数学が苦手な私なので、
子どもと同じ目線で出来るだけわかりやすく分解してみました。
はじめに 三項式とは?
初等代数学における三項式とは、三つの項からなる多項式のことを言うそうです。
初等代数学における三項式(さんこうしき)とは、三つの項からなる多項式を言う。
より一般には、三つの項からなる代数式を単に三項式と呼ぶこともある。
これと対照的に、三項からなる多項式の方は「三項多項式」と呼んで区別する。
引用元:ウィキペディア
三項式と言われてもあまりピンとこないのですが、
三項式の箱だけではなくモンテッソーリの教具をみていると、
はじめて数学の美しさに気付かされます。
モンテッソーリ教具【三項式の箱】の目的
三項式の箱を使ったお仕事の狙いは、
・視覚から3次元を理解する力を養う ・具体物を使いながら、数学的な思考を育てる
ことです。
4歳くらいから夢中になり、一瞬で組み立てていきます。
モンテッソーリ教具の「三項式の箱」は、
a,b,cの3パターンの長さからなる直方体を組み合わせた立方体。
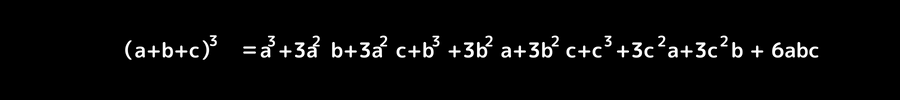
この公式を具体化した教具で、
視覚的に数学的理解をすり込んでいきます。
モンテッソーリ教具【三項式の箱】の仕組み
三項式の箱の中には、赤・青・黄・黒に色分けされた、
27個の直方体でできています。
それぞれの一辺は3つの長さ(a,b,c)の組み合わせで、
これらを組み立て、大きな立方体に仕上げていきます。

縦(a+b+c)× 横(a+b+c)× 高さ(a+b+c)
→ (a+b+c)の3乗が出来上がる立方体の体積



体積を求める意識は子どもにはもちろんないのですが、
数学的な概念を無意識に取り入れると言う意味で、
大きな役割があります。
立方体の6面はどの面から見ても、
赤・青・黄の並びが統一されています。
立体の中も並びは同じで、3次元でこの規則性が統一されています!
木箱の中に入っている直方体の全ては27個
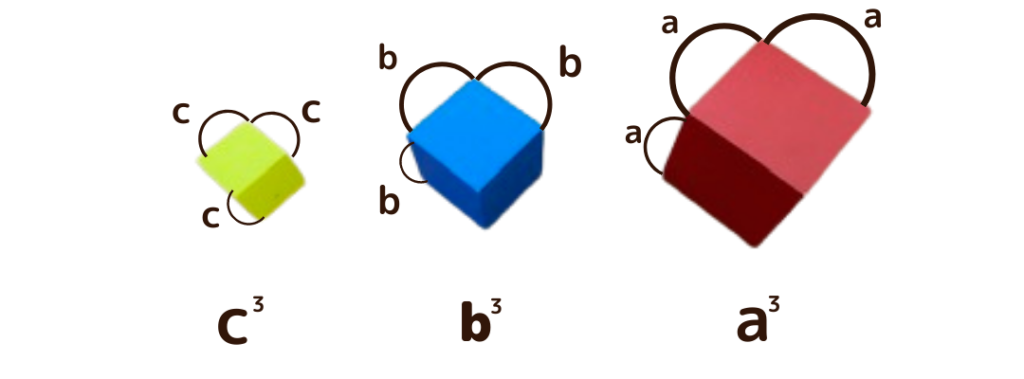

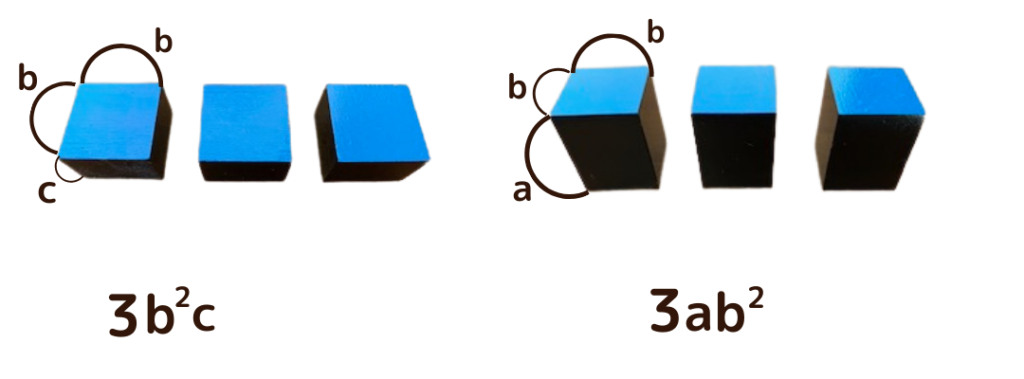
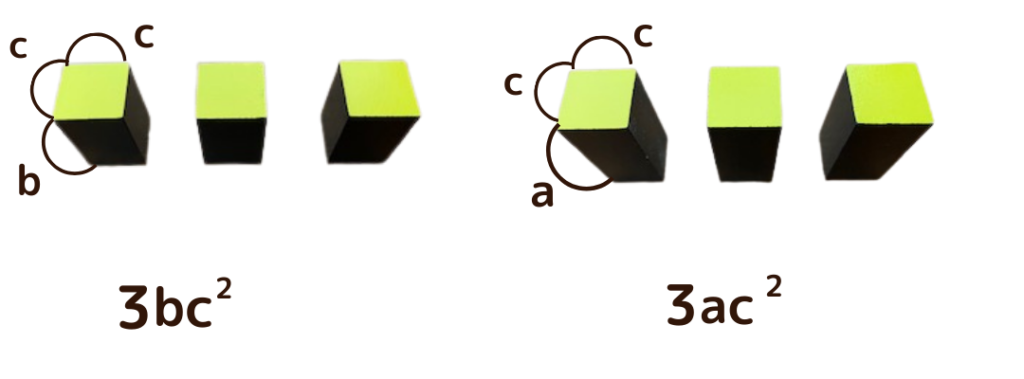

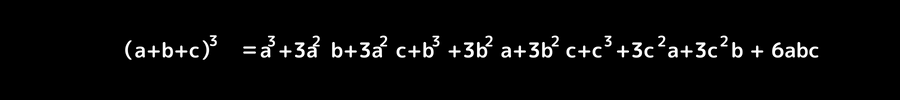

モンテッソーリ教具【三項式の箱】から得る効果
3次元のパズルを楽しむ感覚で、
小学校以降に学ぶ代数へ自然と慣れていくことができます。
まさに具体から抽象への流れがあるので、
理解が深まることが期待されます。
数学の苦手意識が強まる前に、
知育として取り入れるとスムーズです。
モンテッソーリ教具【三項式の箱】まとめ
いかがでしたか?数学が苦手
(=苦手なものは嫌いになってしまう)な母ですが、
子どもに教える際に、
視覚的に説明できる具体物があると良いなという思いもあり、
家でも購入して4歳から始めています。
今は理解しているもいないもわからない状態ですが、
とにかく夢中になって組み立てております。
場所も取らず、見た目もおしゃれな木の教具なので、
一度お試しくださいませ!





